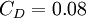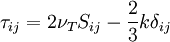Prandtl's one-equation model
From CFD-Wiki
Contents |
Kinematic Eddy Viscosity
Model
Closure Coefficients and Auxilary Relations
where
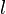 is the turbulent length scale
is the turbulent length scale
References
- Wilcox, D.C. (2004), Turbulence Modeling for CFD, ISBN 1-928729-10-X, 2nd Ed., DCW Industries, Inc..
- Emmons, H. W. (1954), "Shear flow turbulence", Proceedings of the 2nd U.S. Congress of Applied Mechanics, ASME.
- Glushko, G. (1965), "Turbulent boundary layer on a flat plate in an incompressible fluid", Izvestia Akademiya Nauk SSSR, Mekh, No 4, P 13.
Footnotes
- ↑ The exact constant used by Prandtl is currently unknown by the author. Wilcox mentions that other researchers (Emmons 1954 and Glushko 1965) have used a value ranging from 0.07 to 0.09. Prandtl's one equation model can be written in a slightly different way with different constants. For example, CHAM lists the
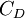 constant as 0.1643, but also uses another definition of the length scale and other constants (see here).
constant as 0.1643, but also uses another definition of the length scale and other constants (see here).
Return to Turbulence modeling

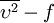 model
model
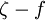 model
model
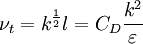
![{{\partial k} \over {\partial t}} + U_j {{\partial k} \over {\partial x_j }} = \tau _{ij} {{\partial U_i } \over {\partial x_j }} - C_D {{k^{{3 \over 2}} } \over l} + {\partial \over {\partial x_j }}\left[ {\left( {\nu + {{\nu _T } \over {\sigma _k }}} \right){{\partial k} \over {\partial x_j }}} \right]](/W/images/math/5/c/1/5c123ddc40f50a9f68c4f07113eebe6f.png)