Algebraic turbulence models
From CFD-Wiki
| (10 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | Cebeci-Smith | + | {{Turbulence modeling}} |
| + | |||
| + | Algebraic [[Turbulence modeling|turbulence models]] or zero-equation turbulence models are models that do not require the solution of any additional equations, and are calculated directly from the flow variables. As a consequence, zero equation models may not be able to properly account for history effects on the turbulence, such as convection and diffusion of turbulent energy. These models are often too simple for use in general situations, but can be quite useful for simpler flow geometries or in start-up situations (e.g. the initial phases of a computation in which a more complicated model may have difficulties). The two most well known zero equation models are the | ||
| + | |||
| + | *[[Baldwin-Lomax model]] and the | ||
| + | *[[Cebeci-Smith model]]. | ||
| + | |||
| + | Other even simpler models, such a models written as <math>\mu_t = f(y^+)</math>, are sometimes used in particular situations (e.g. boundary layers or jets). | ||
| + | |||
| + | The algebraic [[Johnson-King model]] is sometimes called a 1/2 equation model since it incorporates the solution of an ordinary differential equation. | ||
| + | |||
| + | [[Category: Turbulence models]] | ||
Latest revision as of 20:39, 1 April 2007
model
model
Algebraic turbulence models or zero-equation turbulence models are models that do not require the solution of any additional equations, and are calculated directly from the flow variables. As a consequence, zero equation models may not be able to properly account for history effects on the turbulence, such as convection and diffusion of turbulent energy. These models are often too simple for use in general situations, but can be quite useful for simpler flow geometries or in start-up situations (e.g. the initial phases of a computation in which a more complicated model may have difficulties). The two most well known zero equation models are the
- Baldwin-Lomax model and the
- Cebeci-Smith model.
Other even simpler models, such a models written as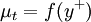 
, are sometimes used in particular situations (e.g. boundary layers or jets).
The algebraic Johnson-King model is sometimes called a 1/2 equation model since it incorporates the solution of an ordinary differential equation.
