Finite element
From CFD-Wiki
Revision as of 21:13, 5 December 2005
The finite element method belongs to the class of weighted residual methods. It is a very powerful method, yet its basic principle is simple and interesting. The differential equation governing the transport of a scalar 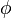 is first written as
is first written as
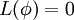
We then assume an approximate solution 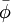 of the form
of the form
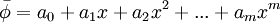
where the a's are unknown coefficients that are to be determined. For an initial value, it is clear that 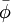 does not satisfy the governing PDE, therfore leaving a residual R defined as
does not satisfy the governing PDE, therfore leaving a residual R defined as

The idea is to drive the residual to zero by performing the convolution of R with a certain weight function 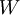
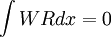
By choosing a succession of weight functions, one can generate as many equations as there are unknowns (the a's) thus yielding a albegraic system of equations.
The method can be viewed as a minimization problem. In fact, most discretization methods have this concept built in which is a fundamental principle in the theory of iterative methods.
