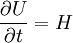Wave propagation
From CFD-Wiki
(Difference between revisions)
| Line 7: | Line 7: | ||
:<math> \frac {\partial U}{\partial t}=H </math> | :<math> \frac {\partial U}{\partial t}=H </math> | ||
The low storage scheme is implemented as follows | The low storage scheme is implemented as follows | ||
| - | :<math> U^{M+1}=U^M+b^ | + | :<math> U^{M+1}=U^M+b^Mdtf^M </math> |
:<math> f^M=a^Mf^{M-1}+H </math> | :<math> f^M=a^Mf^{M-1}+H </math> | ||
| - | + | : where M refers to the stages ,dt is the time step and the coefficients a and b are given by | |
| + | :a[5]={0,-0.41789047,-1.19215169,-1.69778469,-1.51418344} | ||
| + | :b[5]={0.149665602,0.37921031,0.82295502,0.69945045,0.15305724} | ||
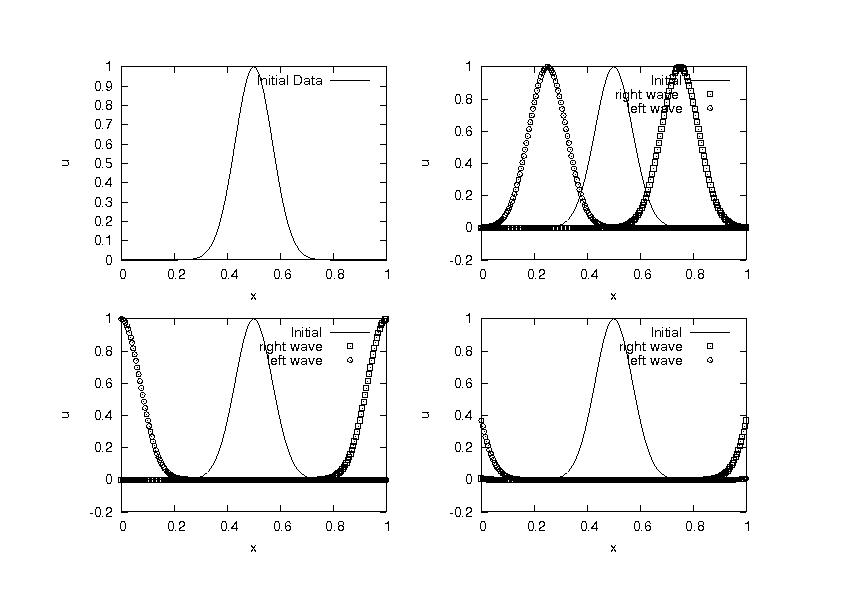
== Sample result == | == Sample result == | ||
[[Image:wp_result.jpg]] | [[Image:wp_result.jpg]] | ||
Revision as of 15:53, 19 September 2005
Contents |
Introduction
The 1-D wave propagation problem is used as a test case for studying the dissipation and dispersion errors in a given finite difference scheme.There are a number of schemes which can be used to solve the problem. The usage of a higher order compact stencil with a low storage 4th order Runga Kutta scheme to solve the current problem is discussed.
Compact scheme
Runga Kutta
Consider
The low storage scheme is implemented as follows

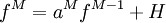
- where M refers to the stages ,dt is the time step and the coefficients a and b are given by
- a[5]={0,-0.41789047,-1.19215169,-1.69778469,-1.51418344}
- b[5]={0.149665602,0.37921031,0.82295502,0.69945045,0.15305724}
Sample result
Reference
Williamson, Williamson (1980), "Low Storage Runge-Kutta Schemes", Journal of Computational Physics, Vol.35, pp.48–56.
Lele, Lele, S. K. (1992), "Compact Finite Difference Schemes with Spectral-like Resolution,” Journal of Computational Physics", Journal of Computational Physics, Vol. 103, pp 16–42.