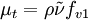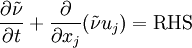Spalart-Allmaras model
From CFD-Wiki
(Difference between revisions)
Revision as of 08:42, 13 September 2005
Spallart-Allmaras model is a one equation model for the turbulent viscosity.
Contents |
Original model
The turbulent eddy viscosity is given by
The constants are
Modifications to original model
Model for compressible flows
There are two approaches to adapting the model for compressible flows. In the first approach the turbulent dynamic viscosity is computed from
where 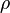 is the local density. The convective terms in the equation for
is the local density. The convective terms in the equation for 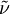 are modified to
are modified to
where the right hand side (RHS) is the same as in the original model.
Boundary conditions
References
- P. R. Spalart and S. R. Allmaras, A One-Equation Turbulence Model for Aerodynamic Flows, AIAA-92-0439, 1992


![\frac{\partial \tilde{\nu}}{\partial t} + u_j \frac{\partial \tilde{\nu}}{\partial x_j} = C_{b1} [1 - f_{t2}] \tilde{S} \tilde{\nu} + \frac{1}{\sigma} \{ \nabla \cdot [(\nu + \tilde{\nu}) \nabla \tilde{\nu}] + C_{b2} | \nabla \nu |^2 \} - \left[C_{w1} f_w - \frac{C_{b1}}{\kappa^2} f_{t2}\right] \left( \frac{\tilde{\nu}}{d} \right)^2 + f_{t1} \Delta U^2](/W/images/math/4/7/6/476216889d1ea0604979b921eae3428c.png)
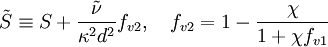
![f_w = g \left[ \frac{ 1 + C_{w3}^6 }{ g^6 + C_{w3}^6 } \right]^{1/6}, \quad g = r + C_{w2}(r^6 - r), \quad r \equiv \frac{\tilde{\nu} }{ \tilde{S} \kappa^2 d^2 }](/W/images/math/0/9/b/09b19885ed6dffe3dec850e2516f1696.png)
![f_{t1} = C_{t1} g_t \exp\left( -C_{t2} \frac{\omega_t^2}{\Delta U^2} [ d^2 + g^2_t d^2_t] \right)](/W/images/math/9/9/3/993b41d0ba795e0b3877d041c4cff1cb.png)