Gradient-based methods
From CFD-Wiki
Shenren CN (Talk | contribs) |
Shenren CN (Talk | contribs) |
||
| Line 13: | Line 13: | ||
Finite difference method is the most straightforward approach, where the sensitivity is calculated through finite difference, using different cost function values corresponding to different design variable input | Finite difference method is the most straightforward approach, where the sensitivity is calculated through finite difference, using different cost function values corresponding to different design variable input | ||
| - | <math>\frac{DJ}{D\alpha_{i}}</math> | + | <math>\frac{DJ}{D\alpha_{i}}=\frac{J}{\delta \alpha}</math> |
Revision as of 03:20, 24 January 2011
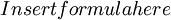As its name means, gradient-based methods need the gradient of objective functions to design variables. The evaluation of gradient can be achieved by finite difference method, linearized method or adjoint method. Both finite difference method and linearized method has a time-cost proportional to the number of design variables and not suitable for design optimization with a large number of design variables. Apart from that, finite difference method has a notorious disadvantage of subtraction cancellation and is not recommended for practical design application.
Suppose a cost function 
is defined as follows,
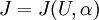
where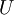 
and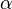 
are the flow variable vector and the design variable vector respectively. 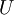and 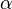are implicitly related through the flow equation, which is represented by a residual function driven to zero.
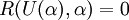
The sensitivity of the cost function with respect to the design variables 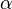, that is 
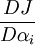, is needed for design purpose. The following is three main methods to obtain this sensitivity.
Finite difference method is the most straightforward approach, where the sensitivity is calculated through finite difference, using different cost function values corresponding to different design variable input
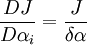
Linearized method:
Adjoint method:
