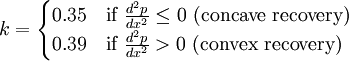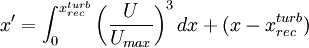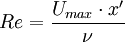Stratford's separation criterion
From CFD-Wiki
(Added formulas for a and b for C'_p > 4/7) |
m (Formatting improvements) |
||
| Line 31: | Line 31: | ||
For <math>C'_p > \frac{4}{7}</math> (velocity ratios <math>\frac{U_{max}}{U} > 1.53</math>) Stratford successfully used the following formula to compute <math>C'_p</math>: | For <math>C'_p > \frac{4}{7}</math> (velocity ratios <math>\frac{U_{max}}{U} > 1.53</math>) Stratford successfully used the following formula to compute <math>C'_p</math>: | ||
| - | <math>C'_p = 1 - \frac{a}{\sqrt{x' + b}}</math>, for <math>C'_p > \frac{4}{7}</math> where the constants a and b are chosen so that the slope and value of <math>C'_p</math> match at <math>C'_p = \frac{4}{7}</math> | + | <math>C'_p = 1 - \frac{a}{\sqrt{x' + b}}</math>, for <math>C'_p > \frac{4}{7}</math> where the constants <math>a</math> and <math>b</math> are chosen so that the slope and value of <math>C'_p</math> match at <math>C'_p = \frac{4}{7}</math> |
| - | To compute <math>a</math> and b for <math>x'_{C'_p = 4/7}</math> the following formulas can be deduced: | + | To compute <math>a</math> and <math>b</math> for <math>x'_{C'_p = 4/7}</math> the following formulas can be deduced: |
<math>b = \frac{3}{14 \cdot \frac{dC'_p}{dx'}|_{C'_p=4/7}} - x'_{C'_p=4/7}</math> | <math>b = \frac{3}{14 \cdot \frac{dC'_p}{dx'}|_{C'_p=4/7}} - x'_{C'_p=4/7}</math> | ||
Latest revision as of 11:10, 11 December 2013
Stratford's separation criterion is an old classical analytical way to assess if a turbulent boundary layer is likely to separate or not. Stratford's criteria says that from the start of the pressure recovery where the max velocity and the minimum static pressure is obtained the boundary layer is on the verge of separation when:
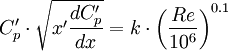
This formula is only valid as long as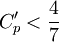 
.
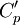is the canonical pressure distribution defined by:
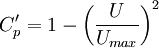
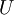is the local velocity and 
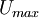is the maximum velocity at the start of the pressure recovery.
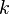is a constant which Stratford used the following values for:
Other researcers have used other values. Cebeci-Smith for example used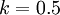 
, which is a bit less conservative than Statford's original values.
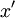is the effective length of the boundary layer. Note that computing 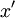can be a bit tricky. If the boundary layer is first accelerated up to the start of the recovery and is assumed to be turbulent all the time a turbulent boundary layer can be assumed to have the followig effective length:
Note that this is only valid if the approaching boundary layer can be assumed to be fully turbulent. If the boundary layer is laminar, or undergoes transition, a different approximations needs to be done.
The Reynolds number above is based on the effective length of the bounday layer 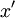and the maximum velocity 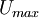at the start of the recovery.
For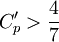 
(velocity ratios 
) Stratford successfully used the following formula to compute :
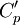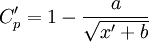, for 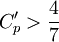where the constants 
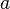and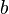 
are chosen so that the slope and value of 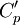match at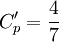 
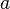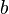To compute and for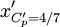 
the following formulas can be deduced:
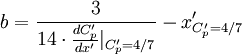
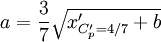
Stratford's separation criteria is known to be conservative. It will most likely predict a bit too early separation.
References
- Stratford, B. S. (1959), "The Prediction of Separation of the Turbulent Boundary Layer", Journal of Fluid Mechanics, Vol. 5, pp. 1-16.
- Cebeci, T., Mosinskis, G. J., and Smith A. M. O (1972), "Calculation of Separation Points in Incompressible Turbulent Flows", Journal of Aircraft, Vol. 9., Sept. 1972, p. 618-624.
