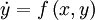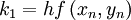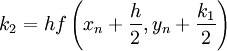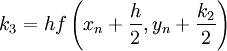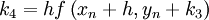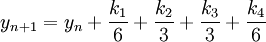Runge Kutta methods
From CFD-Wiki
(Difference between revisions)
| Line 1: | Line 1: | ||
| - | |||
= Forth order Runge-Kutta Method = | = Forth order Runge-Kutta Method = | ||
| Line 11: | Line 10: | ||
::<math>k_4 = hf\left( {x_n + h,y_n + k_3 } \right) </math> | ::<math>k_4 = hf\left( {x_n + h,y_n + k_3 } \right) </math> | ||
::<math>y_{n + 1} = y_n + {{k_1 } \over 6} + {{k_2 } \over 3} + {{k_3 } \over 3} + {{k_4 } \over 6} </math> | ::<math>y_{n + 1} = y_n + {{k_1 } \over 6} + {{k_2 } \over 3} + {{k_3 } \over 3} + {{k_4 } \over 6} </math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | <i> Return to [[Numerical methods | Numerical Methods]] </i> | ||
Revision as of 00:49, 1 November 2005
Forth order Runge-Kutta Method
The forth order Runge-Kutta method could be summarized as:
Algorithm
Return to Numerical Methods