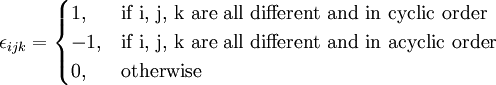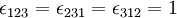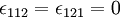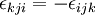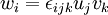Alternating tensor
From CFD-Wiki
(Difference between revisions)
| (One intermediate revision not shown) | |||
| Line 1: | Line 1: | ||
| + | The alternating tensor, also known as '''Levi-Civita''' symbol is defined by | ||
| + | |||
:<math> | :<math> | ||
\epsilon_{ijk} = \begin{cases} | \epsilon_{ijk} = \begin{cases} | ||
| Line 5: | Line 7: | ||
0, & \mbox{otherwise} | 0, & \mbox{otherwise} | ||
\end{cases} | \end{cases} | ||
| + | </math> | ||
| + | |||
| + | Thus | ||
| + | |||
| + | :<math> | ||
| + | \epsilon_{123} = \epsilon_{231} = \epsilon_{312} = 1 | ||
| + | </math> | ||
| + | |||
| + | :<math> | ||
| + | \epsilon_{321} = \epsilon_{132} = \epsilon_{213} = -1 | ||
| + | </math> | ||
| + | |||
| + | If any index is repeated then the value is zero, e.g., | ||
| + | |||
| + | :<math> | ||
| + | \epsilon_{112} = \epsilon_{121} = 0 | ||
| + | </math> | ||
| + | |||
| + | If any two indices are interchanged then the sign changes, e.g., | ||
| + | |||
| + | :<math> | ||
| + | \epsilon_{kji} = -\epsilon_{ijk} | ||
| + | </math> | ||
| + | |||
| + | This tensor is useful in defining the cross product of two vectors. If <math> w := u \times v</math>, then | ||
| + | |||
| + | :<math> | ||
| + | w_i = \epsilon_{ijk} u_j v_k | ||
</math> | </math> | ||
Latest revision as of 04:38, 20 September 2005
The alternating tensor, also known as Levi-Civita symbol is defined by
Thus
If any index is repeated then the value is zero, e.g.,
If any two indices are interchanged then the sign changes, e.g.,
This tensor is useful in defining the cross product of two vectors. If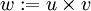 
, then
